GARIS DAN SUDUT

BAB 2 : Hubungan Antar Garis

2.1 Hubungan Titik dan Garis

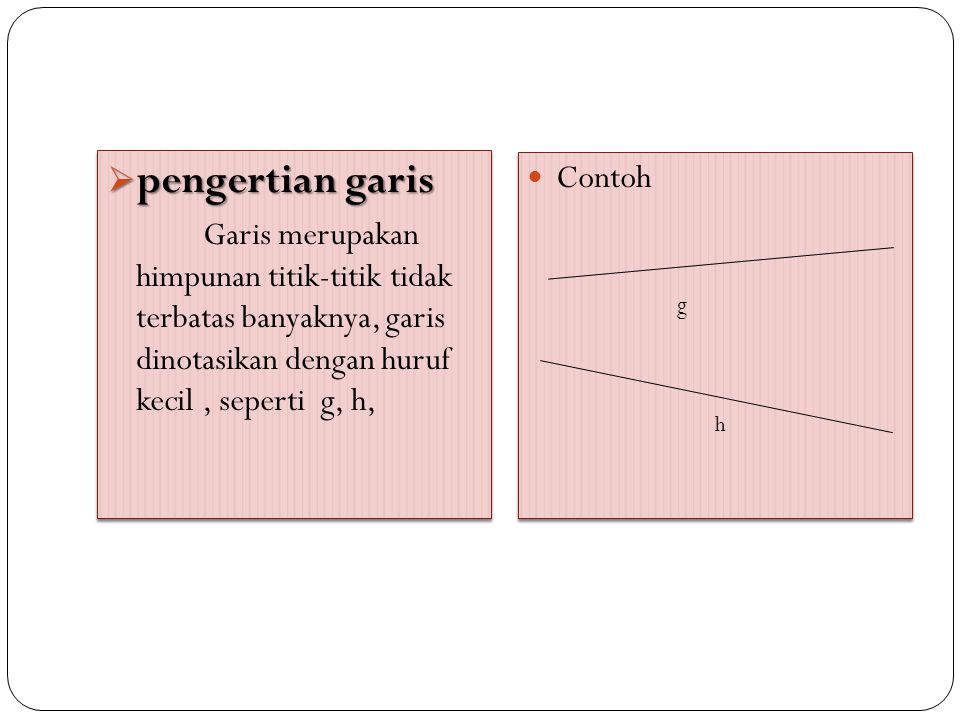
Gambar Pengertian Garis

2.1.1 Titik terletak pada garis

Titik terletak pada garis apabila titik tersebut berada pada garis sehingga titik tersebut menjadi bagian dari garis tersebut. Contoh : titik C berada tepat terletak pada garis f. Titik C merupakan bagian dari garis f.

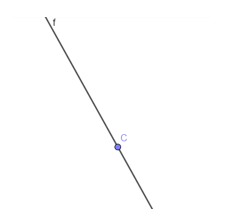
Gambar Titik terletak pada Garis

2.1.2 Titik terletak di luar garis

Titik yang tidak terletak pada garis tersebut sehingga titik terebut tidak menjadi bagian dari garis tersebut dan titik tersebut terletak di luar garis. Contoh : titik E terletak di luar garis sehingga titik E tidak menjadi bagian garis f.

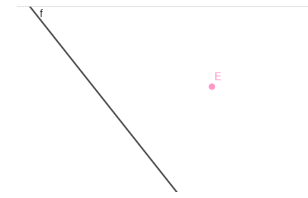
Gambar Titik di luar Garis

2.2 Hubungan Garis dan Bidang

2.2.1 Garis terletak pada bidang

Jika suatu garis terletak pada bidang sehingga garis tersebut menjadi bagian dari bidang. Contoh : garis l terletak pada bidang M sehingga garis l menjadi bagian dari bidang M dan juga membagi bidang menjadi dua bagian bidang.

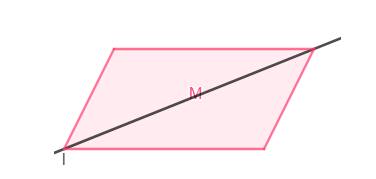
Gambar Garis Terletak Pada Bidang

2.2.2 Garis tidak pada bidang

Letak suatu garis di luar bidang apabila garis tersebut tidak menjadi bagian bidang. Contoh : garis k tidak terletak pada bidang atau di liar bidang letaknya dan tidak menjadi bagian dari bidang M.

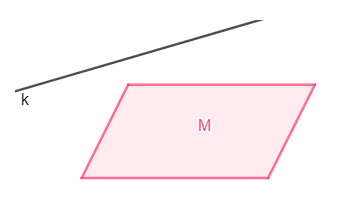
Gambar Garis Tidak Terletak Pada Bidang

2.2.3 Garis menembus/ memotong bidang

Garis menembus/memotong bidang jika persekutuan antara garis dan bidang adalah sebuah titik. Contoh garis i menembus/ memotong bidang M sehingga muncul persekutuan antara garis i dengan bidang M, yakni titik G.

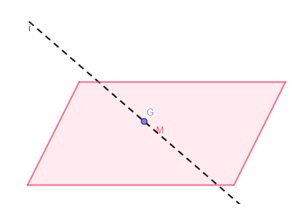
Gambar Garis Memotong/Menembus Bidang

2.3 Hubungan Antar Dua Garis

2.3.1 Dua Garis Sejajar

Dua garis sejajar di bidang jika terdapat dua garis yang terletak pada satu bidang dan apabila dua garis tersebut diperpanjang maka garis tersebut tidak akan pernah berpotongan. Notasi dari dua garis sejajar ini adalah //.

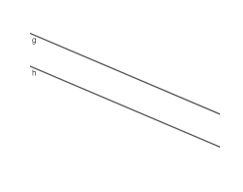
Gambar Dua Garis Sejajar

Pada gambar di atas terdapat dua garis, yakni garis g dan garis h yang dikatakan dua garis sejajar karena garis g dan garis h tersebut diperpanjang maka dua garis tersebut tidak akan pernah bertemu atau pun berpotongan. Maka g//h.

2.3.2 Dua Garis Saling Berpotongan

Dua garis dikatakan saling berpotongan apabila mempunyai titik persekutuan, titik persekutuan ini biasa disebut titik potong. Notasi dua garis saling berpotongan adalah ×.

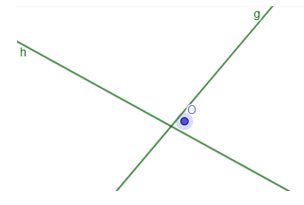
Gambar Dua Garis Saling Berpotongan

Garis g dan garis h adalah garis berpotongan karena memiliki titik potong di O, sehingga g×h.

Jika titik potong garis g dan garis h membentuk sudut siku- siku maka garis g dan garis h dikatakan dua garis yang berpotongan tegak lurus. Notasi dari berpotongan tegak lurus, yaitu ⊥. Sehingga dapat dituliskan g ⊥ h.

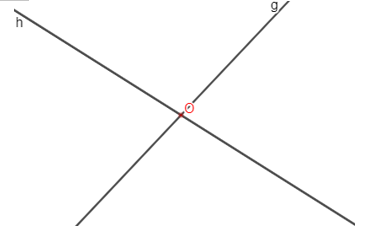
Gambar Dua Garis Berpotongan Tegak Lurus

2.3.3 Dua Garis Berhimpit

Dua garis berhimpit adalah keadaan dimana terdapat kedua garis saling menempel dan searah sehingga mempunyai tak hingga titik persekutuannya. Oleh sebab itu, terkadang dua garis yang berhimpit terlihat seperti hanya ada satu garis.

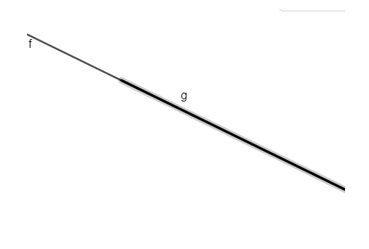
Gambar Dua Garis Berhimpit

Terdapat garis f dan garis g yang berhimpit dikarenakan kedua garis tersebut saling menempel dan terlihat seperti satu garis serta mempunyai tak hingga titik persekutuan.

2.4 Ringkasan

• Garis adalah kumpulan titik – titik yang tak terhingga banyaknya.
• Titik terletak pada garis apabila titik tersebut berada pada garis sehingga titik tersebut menjadi bagian dari garis tersebut.
• Titik yang tidak terletak pada garis tersebut sehingga titik terebut tidak menjadi bagian dari garis tersebut dan titik tersebut terletak di luar garis.
• Garis terletak pada bidang apabila jika suatu garis terletak pada bidang sehingga garis tersebut menjadi bagian dari bidang.
• Garis tidak terletak atau di luar bidang apabila jika letak suatu garis di luar bidang apabila garis tersebut tidak menjadi bagian bidang.
• Garis menembus/memotong bidang jika persekutuan antara garis dan bidang adalah sebuah titik.
• Dua garis sejajar di bidang jika terdapat dua garis yang terletak pada satu bidang dan apabila dua garis tersebut diperpanjang maka garis tersebut tidak akan pernah berpotongan.
• Dua garis dikatakan saling berpotongan apabila mempunyai titik persekutuan, titik persekutuan ini biasa disebut titik potong.
• Dua garis berhimpit adalah keadaan dimana terdapat kedua garis saling menempel dan searah sehingga mempunyai tak hingga titik persekutuannya.

2.5 Latihan

1. Perhatikan gambar di bawah ini ! Sebutkan pasangan garis mana yang saling sejajar, berpotongan dan berhimpit !


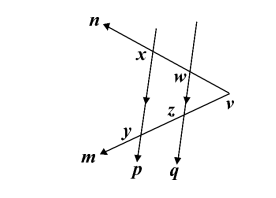
Penyelesaian :

Pasangan garis yang sejajar, yakni garis p dan garis q, garis y dan garis z, garis x dan garis w. Pasangan garis yang berpotongan, yakni garis x dan n, garis w dan garis n, garis y dan garis m, garis z dan garis m. Pasangan garis yang berhimpit, yakni garis x dan y, garis y dan garis p, garis w dan garis z, garis z dan garis q.

2. Jelaskan perbedaan dua garis berpotongan dengan dua garis berpotongan tegak lurus besertakan gambarnya !

Penyelesaian :

Perbedaan dua garis berpotongan dengan dua garis berpotongan tegak lurus adalah kalau dua garis berptongan tegak lurus titik potongnya membentuk sudut siku- siku sedangkan dua garis yang berpotongan saja titik potongnya tidak membentuk siku- siku.

2.6 Evaluasi

Pilihan Ganda

1. Perhatikan gambar berikut.


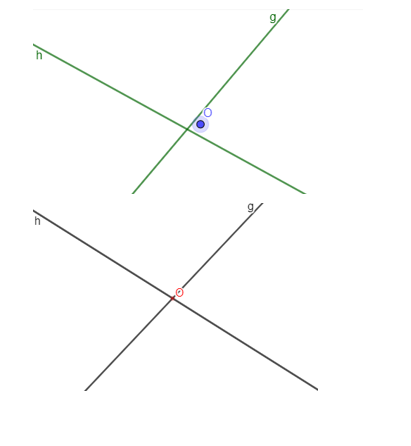
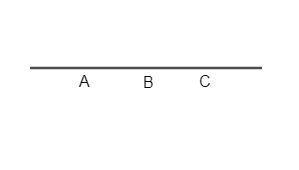
Banyak ruas garis berbeda dari gambar di atas adalah . . .

1. 2
2. 3
3. 4
4. 5
2. Sebuah garis dan bidang tidak terletak pada bidang yang sama dan tidak berpotongan, maka irisan keduanya menghasilkan...
1. sebuah titik
2. tak hingga titik
3. dua titik
4. himpunan kosong
3. Terdapat dua garis saling berpotongan dan tidak berhimpitan, maka perpotongannya berbentuk...
1. titik
2. bidang
3. garis
4. ruang
4. Pernyataan yang salah dari pendapat berikut adalah . . . li>
   1. dua garis sejajar tidak mempunyai titik potong
   2. garis k sejajar bidang M apabila garis-garis yang terletak pada bidang M tidak berpotongan dengan garis k
   3. garis k tegak lurus bidang M apabila garis k tegak lurus garis-garis yang terletak pada bidang M.
5. Jika suatu garis terletak pada bidang sehingga garis tersebut menjadi bagian dari bidang disebut...
1. garis memotong bidang
2. garis terletak di luar bidang
3. garis menembus bidang
4. garis terletak pada bidang

Esai

1. Hubungan antara garis dan bidang ada tiga, yaitu .....
2. Bagaimana keberadaan garis dengan titik, garis dengan bidang, dan garis dengan garis lainnya? Jelaskan !
3. Jelaskan menurut pendapat kalian apakah boleh kita mengatakan
1. Garis adalah kumpulan titik-titik ?
2. Bidang adalah kumpulan titik-titik ?
3. Bidang adalah kumpulan garis-garis ?
4. Ruang adalah kumpulan garis-garis ?
4. Gambarlah limas seempat ABCD.T
1. Sebutkan semua ruas garis yang saling sejajar.
2. Sebutkan semua ruas garis yang saling berpotongan
3. Adakah dua garis yang saling tegak lurus? Jelaskan
4. Adakah dua garis yang saling bersilangan? Jelaskan.
5. Perhatikan gambar balok ABCD.EFGH berikut.


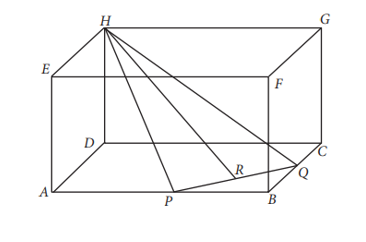
Diketahui titik P berada di tengah-tengah AB , titik Q di tengah-tengah BC , dan titik T di tengah-tengah PQ . Hubungkan titik H dangan titik R. Jika HR diperpanjang, maka apakah akan memotong perpanjangan FB ? Jelaskan dan tunjukkan!